
What is a Smith Chart?
February 10, 2023Introduction
The Smith chart is a useful graphical tool to convert between impedances and reflection coefficients. It may also be used to solve impedance-matching problems. It can be thought of as a polar reflection coefficient chart with overlaid impedance curves.

Figure 1 – Smith Chart
Reflection Coefficients
The reflection coefficient of an impedance can be measured with a vector network analyzer.
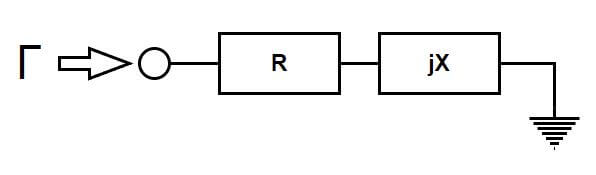
Figure 2 – Measured Reflection Coefficient
That reflection coefficient will be: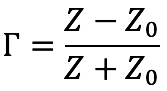
where Z is the complex impedance R+jX and Z0 is the characteristic impedance of the source.
For Z = Z0, the reflection has a magnitude of zero, a dot at the center of the smith chart. For Z = 0, the reflection is 1∠0 or Cartesian 1,0.
For Z = ∞, the reflection is 1∠180 or Cartesian -1,0.
For Z = 23+j75, the reflection coefficient is 0.762∠64 or 0.333+j0.685
These four reflections are plotted on the polar plot in Figure 3.
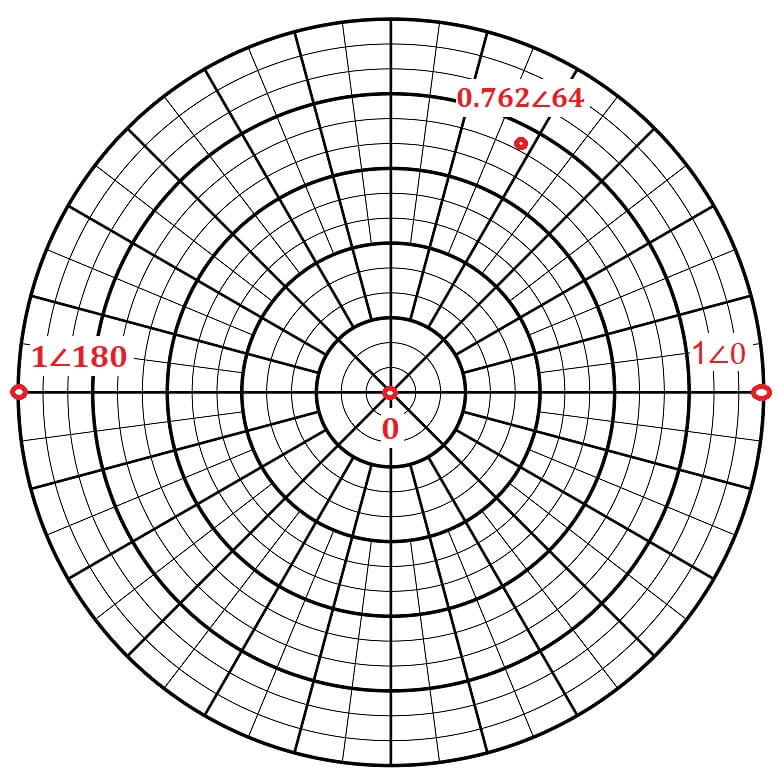
Figure 3 – Polar Reflection Coefficients
Building the Smith Chart
These reflection coefficients were calculated from Equation 1. Using this equation, we could choose a real part of the impedance, the resistance, hold it constant, and then let the imaginary part, the reactance, go from -∞ to +∞ and draw the result on the polar plot.
With the resistances normalized to 50 ohms, we can draw these circles of constant resistance for 10, 20, 50, 100, and 200 ohms, or 0.2, 0.4, 1, 2, and 4 when normalized.
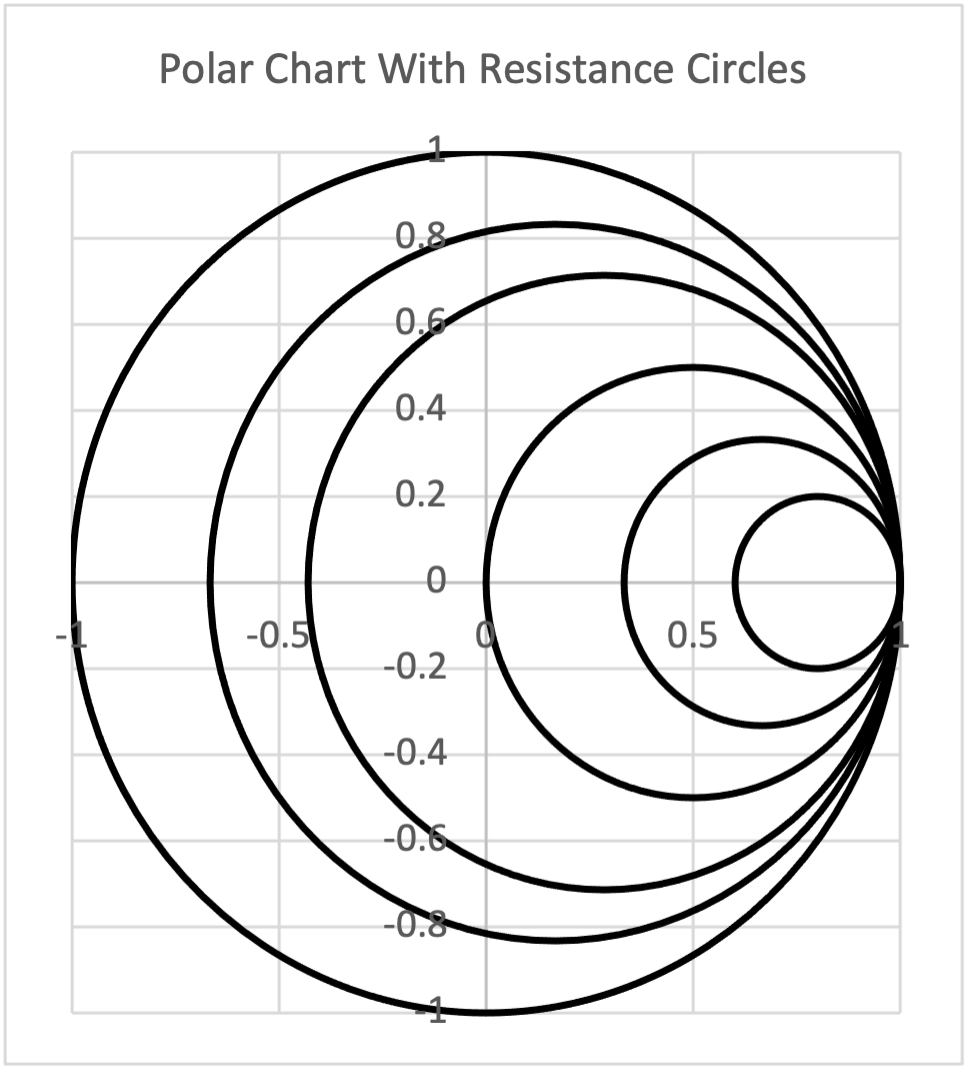
Figure 4 – Polar Chart with Resistance Circles
The circles are centered at R/(R+1),0, with a radius of 1/(R+1), where R is the normalized value.
We can then choose reactances and sweep the resistance from -∞ to +∞ to obtain arcs of constant reactance.

Figure 5 – Completed Smith Chart
After the circles of resistance and curves of reactance are added to the polar chart and labeled, one can locate the reflection coefficient of any impedance by inspection.
Impedance Matching
You can use a Smith chart to assist in impedance matching with lumped elements or transmission lines. For instance, if we start at an impedance of 20+j35Ω and want to match to 50Ω at 500 MHz, we can use a shunt capacitor followed by a series capacitor. To make the graphical method simpler, a mirror image of the resistance and reactance circles and arcs must be added (in blue in Figure 6) to represent shunt conductance and susceptance.
The first step is to add a shunt term to provide enough susceptance to get to the constant 50Ω resistance circle. To get from 20+j35 to the constant 50 ohm resistance circle, we added 11.9 *10-3 mhos of capacitive susceptance, or 3.8 pF at 500 MHz. From there, a negative reactance of 39.8 ohms is needed to get to the center of the Smith chart, or 8.0 pF at 500 MHz. These manipulations can be done directly on a Smith chart, but it is much simpler to use the Smith program designed by Prof. Fritz Dellsperger at www.fritz.dellsperger.net. The demo version is free of charge, while the licensed version has more features. It is very instructive to see how the addition of series or shunt elements moves the chart’s impedance.
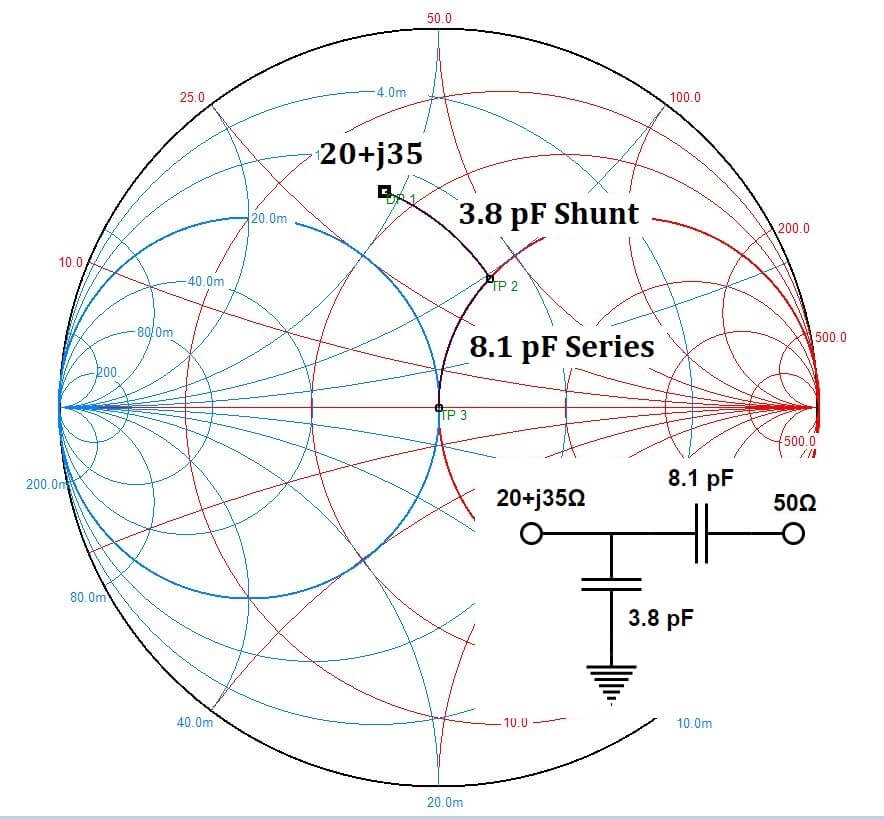
Figure 6 – Matching
This same match could be accomplished with a series capacitor to get to the 0.02 m-mho conductance circle (1/50Ω), followed by a shunt capacitor to get to the middle of the Smith chart. 30.1 pF and 7.8 pF respectively, as in Figure 7.
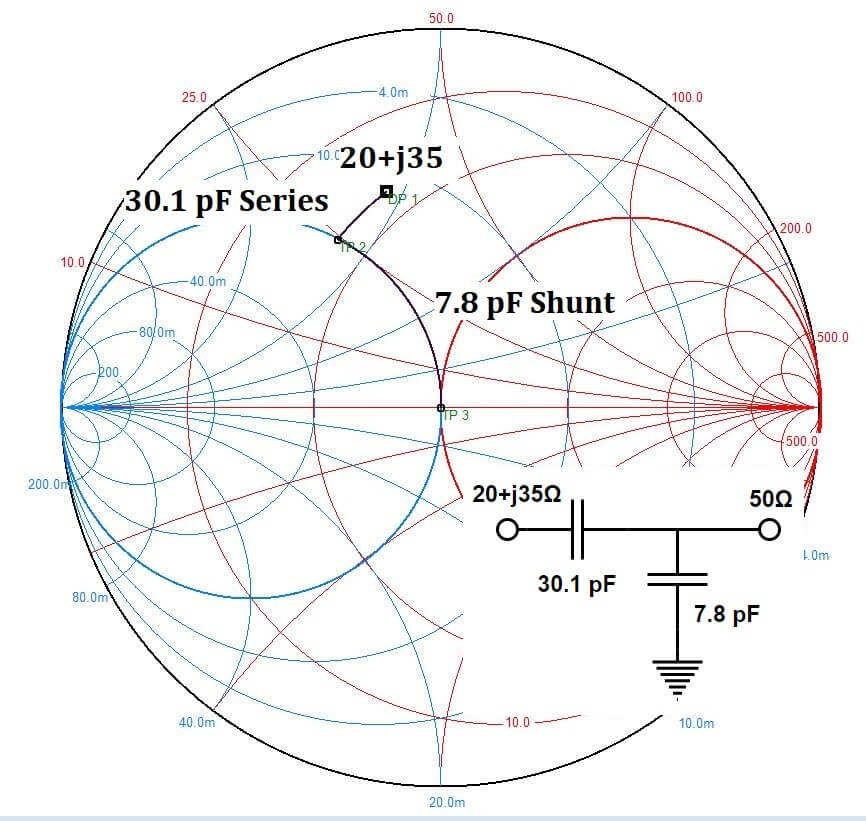
Figure 7 – Alternate Match
Finally, you could use a 5.3 pF series capacitor to get to the 0.02 m-mho (1/50Ω) conductance circle on the other side, and then use a shunt 13 nH inductor, as in Figure 8, to get to the middle of the Smith Chart. The possibilities are endless, but the matching bandwidth will become narrower and narrower as more distance is traversed on the chart.
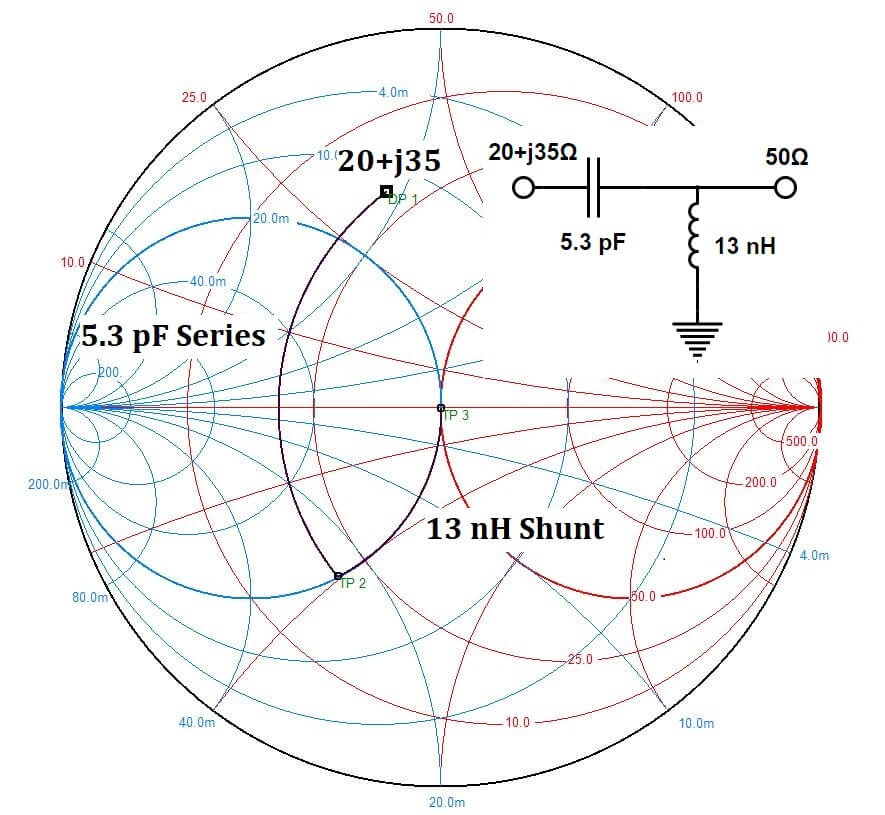
Figure 8 – LC Match
Transmission Line Matching
Transmission lines can also be used for impedance matching. In a special case, if it is necessary to match from one real impedance to another, such as 50Ω to 100Ω, a quarter wavelength transmission line with impedance of the square root of the product of the two, or 70.7Ω will work.
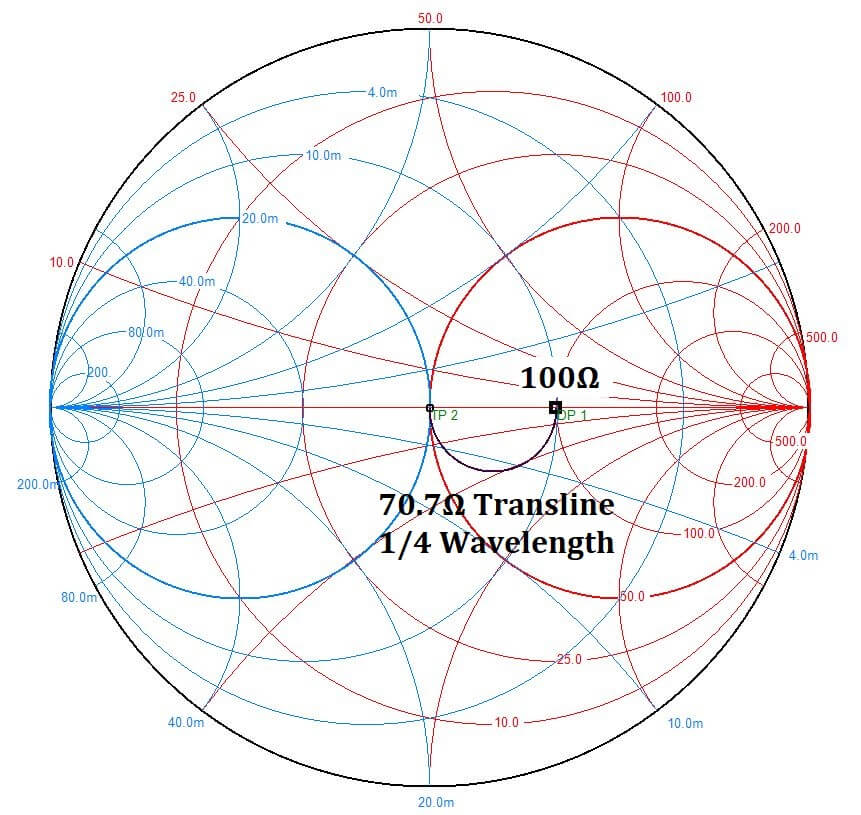
Figure 9 – Series Transmission Line Match
A Wilkinson power splitter is comprised of two, quarter wavelength 70.7Ω transmission lines, which are joined together at one end. Each 50Ω terminated line looks like 100Ω where they are joined together, resulting in an effective 50Ω impedance.
In general, a series transmission line will rotate any real impedance Z clockwise around impedance and a 50Ω transmission line will rotate an impedance around the center of the Smith chart.
For a large change in impedance, such as from 50Ω to a 2Ω LDMOS power amplifier gate, make the transition in two or more steps to maximize the match bandwidth. A quarter wavelength 6Ω line, followed by a quarter wavelength 30Ω line, is preferrable to a single quarter wavelength 10Ω line. The bandwidth is superior, as shown in Figure 11.
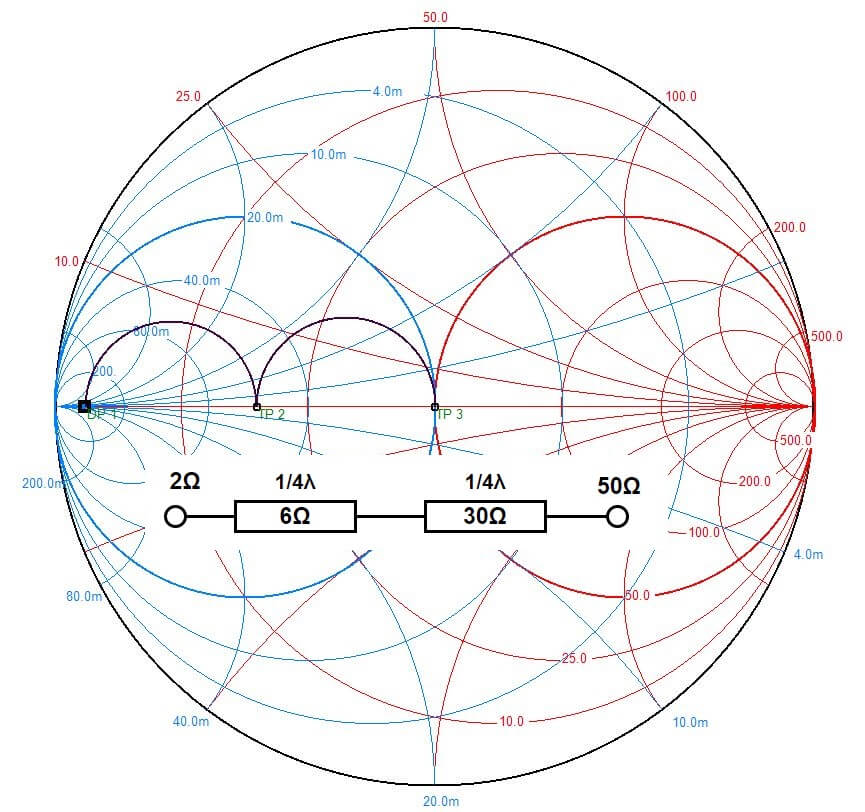
Figure 10 – Transmission Line Match
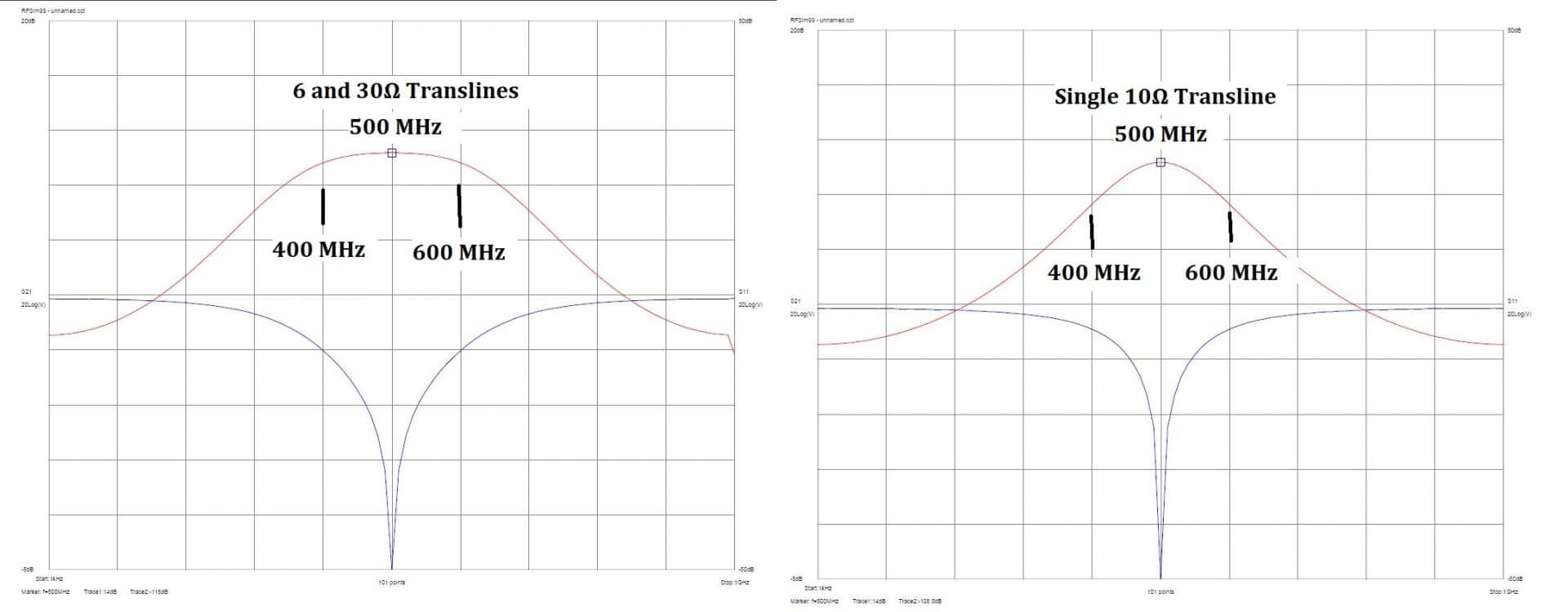 Figure 11- Two vs One Transmission Line Match
Figure 11- Two vs One Transmission Line Match
Summary
The Smith chart is a very convenient tool to graphically calculate and visualize impedance transformations with lumped elements or transmission lines. There are many lumped element solutions for any given matching problem, and transmission lines—particularly quarter wavelength lines— may be used singly or in cascade to match two real impedances.
The chart is educational and helps provide an intuitive understanding of impedance transformations.
Related Post

What is a Smith Chart?
February 10, 2023
The Smith chart is a very convenient tool to graphically calculate and visualize impedance transformations with lumped elements or transmission lines.

What are S-Parameters?
January 31, 2023
The measurement of all four S-parameters over a frequency represents a full characterization of any linear device. S-parameter data saved as a touchstone file may be imported into most linear simulators to demonstrate the device performance within a larger system.
What is a Waveguide?
January 31, 2023
A waveguide is rectangular, circular, or oval “pipe” filled with air or dielectric material which is capable of conveying RF energy. The physical implementation of the structure determines the frequencies which may be transported. Many Eigenmodes are possible, but the lowest order is almost always used. Equations for the calculation of these modes for rectangular waveguides are detailed below. A chart of common commercially available waveguides is included at the document’s conclusion.
What is an Automatic Calibration Module?
January 6, 2023
What is an ACM? An Automatic Calibration Module, or ACM, is used to perform user calibration on a Copper Mountain Technologies Vector Network Analyzer (VNA). This is the calibration which is performed prior to making a series of measurements, not the one performed on an annual or semi-annual basis at a calibration laboratory. The ACM presents a series of calibration standards to the VNA – that is, one or more Opens, Shorts, Loads, and a Thru – to complete a SOLT (Short/Open/Load/Thru) full 2-port calibration, or a SOL 1-port calibration. A simplified block diagram is shown in Figure 1. Figure 1 - ACM Block Diagram A mechanical calibration kit contains individual Open, Short, Load, and Thru calibration pieces, which must be attached to the VNA one after another. A calibration kit definition file informs the VNA of what reflection coefficient each piece should exhibit at each frequency, and calibration is calculated by comparing measured values to actual values. In contrast, the Short, Open, Load, and Thru in the ACM have been precisely characterized at the CMT factory and the results are stored in its non-volatile memory. This is much more accurate than the typical polynomial curve fit definition of the mechanical kit. The ACM completes the calibration process with a single connection to the test cables, automatically cycling through the internal calibration standards. How is it Used? A USB cable must be connected between the ACM and the PC running the VNA software to use the ACM. The ACM is then attached to the test cables and either 1-port, 2-port, or 2-port one-path calibration methods are chosen under the Calibration/Autocal menu. The ACM may be attached to the test cables in either direction, with Port A on the Port 1 test cable, or with Port B when the orientation option is set to AUTO. The operating frequency range of the ACM is printed on the label. When using an ACM, make sure that the VNA frequency range is within the range printed on the ACM. Leave the thermo compensation function ON, as this will provide more accurate calibration when ambient conditions change. Figure 2 - 8 GHz 2-Port ACM Allow the calibration to complete, and then COR should appear in the lower-left corner of the VNA UI screen. The calibration type should be added at the end of the trace definition in the upper left corner – [F1], [F2], and [OP] for full 1-port, 2-port, and one-path 2-port calibration respectively. For 4-port calibration, the ACM4509 AND ACM4520 are 9 and 20 GHz 4-port models respectively. They are capable of performing 1-, 2-, 3-, or 4-port calibration as needed. The Confidence Check feature, which may be enabled in the Automatic Calibration menu, helps verify the integrity of the test cables. After pressing the Confidence Check button in the User Interface, an approximately 20 dB attenuator is connected internally between the A and B ports of the ACM and a precision factory measurement of that same attenuator is loaded into the active trace memory. The memory trace will normally be covered by the active measurement, so it is best to subtract the live measurement from the memory trace by navigating to Display>Memory>Data Math>Data / Memory. Set the scale to a low value, such as 0.05 dB/Div, for a magnitude reading and then move the ACM from side to side to flex the test cables slightly. There should be very little movement of the displayed difference. If wild movement is seen, then the test cables are either loose or defective. Defective cables should be discarded immediately. Figure 3 - ACM Connection for 1-Port Calibration, Load Unused Port Figure 4 - ACM Connection for 2-Port Calibration Why Use an ACM? The measurement accuracy of the VNA depends on the quality of the user calibration. You can best understand the quality of calibration by examining the residual errors which remain after the calibration is performed. The 12-term error model is generally used to characterize these errors – six terms for forward measurements, such as S11 and S21, and six for the reverse, S22 and S12. These errors are depicted in the S-parameter network diagrams shown below. Figure 5 - 12 Term Error Model, Forward and Reverse The actual Device Under Test (DUT) S-parameters are shown in the grey box, and the error vectors appear on either side of it. These errors are: Table 1 - 12 Term Errors After calibration, these errors are greatly reduced but are not zero. The remaining errors are called residual errors. For instance, the raw directivity of the directional bridge in the VNA might be 18 dB, but after calibration with an ACM, it might be 46. The Importance of Residual Directivity The directional bridge in the VNA has four ports: an input, an output, a forward sample port, and a reverse sample port. When a forward traveling signal passes through the bridge, the forward port should have an attenuated version of this signal exiting it, assuming 20 dB coupling attenuation for example. A reverse traveling signal should cause a 20 dB down signal to appear on the reverse sample port. Ideally, there would be no signal on the reverse sample port when there is only a forward traveling wave passing through the bridge. As no bridge is ideal, a leakage signal will be present as shown in Figure 6. If the normal coupling is 20 dB and the leakage signal is 35 dB, then we say the bridge has 15 dB of directivity. To understand the importance of the quality of the calibration kit, consider the following: to improve the directivity, you would have the VNA produce a signal and terminate it by attaching the calibration load to the output port. Theoretically, there would be only a forward traveling signal leaving the VNA and no reflection from the load, hence no reverse traveling signal. The leakage signal could then be measured on the reverse sample port and simply subtracted from all subsequent measurements. The residual (corrected) directivity would be infinite! Unfortunately, the assumption that there is no reflection from the calibration load is incorrect. A very expensive (~$6k) 26 GHz, 3.5mm calibration load will have worst case return loss of about 30 dB, so there will be a reflected signal, 30 dB down entering the port. This will show on the reverse sample port. The residual directivity of the bridge after calibration will therefore be no better than 30 dB. Figure 6 - Bridge with Leakage Signal Because the ACM has a stable, temperature-compensated, data-based calibration load, the residual directivity after calibration is 46 dB, much better than 30 dB. Residual Errors and Reflection Uncertainty The other error terms are corrected to the much smaller residual values based on the quality of the calibration standards within the ACM. The uncertainty of VNA measurements depends on the values of these residual errors. A typical reflection uncertainty chart after ACM calibration is shown in Figure 7. Figure 7 - Reflection Uncertainty The floor for reflection measurement accuracy is determined by the residual directivity error. The quality of the calibration load is very important. To put it another way, 1-port reflection measurements are not noise limited, but rather interference limited by the residual directivity. The reflection uncertainty curve above is only valid for calibration with an ACM. If using a mechanical kit with a 30 dB return loss calibration load instead, the above curve would be shifted 16 dB to the right and the uncertainty for a -20 dB reflection measurement would be about ± 3 dB instead of ± 0.6. From EUROMET [1], the equation for the approximate uncertainty of a reflection measurement in terms of the residual errors is (in linear terms): Where Sii is the measured reflection T is the Residual Reflection Tracking M is the Residual Source Match L is the Residual Load Match And R accounts for random factors such as connector repeatability The Load match term, L, only applies for reflection measurements of a DUT, which is terminated on the other side by the opposite port of the VNA and insertion loss through the DUT is low (S12 = S21≈1). Residual reflection tracking and source match dominate for high reflection, and residual directivity dominates for low reflection measurements. Residual directivity, D, is approximately equal to the calibration load uncertainty; 30 dB for the expensive mechanical kit and 46 dB for the ACM. Residual source match is approximately equal to the weighted square root of the sum of the squares of the calibration load uncertainty and the angular phase error (radians) of the Open and Short calibration standards. Residual load match is approximately equal to the residual source match for a 2-port calibration with unknown thru. The uncertainties of the calibration standards determine the residual errors and how those residual errors affect the final reflection measurement uncertainty. A more thorough treatment of VNA metrology is given in [2]. Residual Errors and Transmission Uncertainty A typical transmission measurement uncertainty chart after ACM calibration (CMT model S5065) is shown in Figure 8. Figure 8 - Transmission Uncertainty, Model S5065 For transmission measurements, the approximate measurement uncertainty is given by: Where: T is the Residual Transmission Tracking error M is a residual error due to DUT mismatch I is the residual Isolation error R includes a number of random factors but is dominated by the noise floor for small reflections Residual transmission tracking is proportional to the product: Where: µ1 is Residual Source Match L2 is Raw Load Match µ2 is Residual Load Match L1 is Raw Source Match Raw source and load match are properties of the VNA hardware, and residual source and load match are approximately equal to the uncertainty of the calibration load standard. The raw source and load match of the VNA should be reasonable, but the two products above are dominated by the small residual values. For a well-matched DUT, the M term may be ignored, and the port-to-port isolation of the VNA is normally below thermal noise in 10 Hz bandwidth, so it can also be ignored. The R term is mostly trace noise due to proximity of the measurement to the receiver noise floor. The uncertainties of the calibration standards affect uncertainty of transmission measurements over a broad range from about 0 to -60 dB. Below -60 dB, random noise introduced by the receiver noise floor dominates, and above 0 dB, receiver compression introduces errors. Receiver compression errors may be avoided by reducing the stimulus power for amplifier measurements. Again, the quality of the calibration kit is important for precise transmission measurements. Adding Adapters to the ACM Normally, you would use an ACM that matches the connectors of the test cables. For instance, an ACM with female-to-female N connectors would be selected for use with test cables having male N connectors. Sometimes, adapters are added to the ACM to allow for calibration using test cables with non-matching connectors. User Characterization can be performed on the ACM to allow for this. As an example, use test cables that have 3.5mm male connectors and an ACM that has female N connectors. Place the N Male to 3.5mm female adaptors on the ACM and torque them appropriately. Calibrate the ends of the test cables using a 3.5mm calibration kit, another ACM, or a good mechanical kit. Make sure the frequency range is appropriate for the adapters and set the number of points to 1601. Attach the test cables to the ACM with adapters using proper torque. In the VNA User Interface under Calibration/AutoCal, select Characterization and change it from “factory” to one of three user characterizations. Press the Characterize AutoCal Module button, allow the calibration to complete, then fill out the information on the dialogue screen which will automatically appear. After User Characterization, the adapters should be left on the ACM. If they need to be removed and then re-attached, the user characterization should be repeated. Conclusion The accuracy of the VNA measurement greatly depends on the quality of the calibration kit in use, especially for 1-port reflection measurements. Because of its thermally compensated, data-based internal calibration standards, the ACM delivers consistently superior results as compared to calibration using even a very high-grade mechanical calibration kit. In addition, the Confidence Check feature provides a fast and easy method to verify the robustness of the calibration and test set-up. For precision VNA measurement, an ACM is required. 2 and 4-Port ACM modules can be found on the CMT website here. References [1] EURAMET, “Guidelines on the Evaluation of Vector Network Analyzers”, Euramet cg-12 Version 2.0, 3/2011. [2] Brian Walker, Copper Mountain Technologies, “Introduction to the Metrology of VNA Measurement”, May 31st, 2022.

What Makes a Good VNA?
February 14, 2018
Everyone knows that a good VNA should have both excellent hardware performance and an easy to use software interface with useful post-processing capabilities. There are numerous VNAs in the market with different performance levels; some of them are economy grade, and others are truly laboratory test grade. What separates the two?


