What is Thermal Noise?
March 22, 2023First start with Boltzmann’s constant:![]()
Boltzmann’s constant, k, gives the proportionality of the average kinetic energy of a particle in a system of particles at temperature K (degrees Kelvin). There will exist a statistical distribution of particles with higher or lower energy, but the average over a sufficiently great number of particles is useful for further calculations.
Charges within a resistor move about with thermal kinetic energy. If we consider a leaded resistor, then the axial component of current movement generates a voltage on the leads. This random axial charge movement creates an AC noise voltage on the resistor leads equal to:![]()
Where k is Boltzmann’s constant
T is the Kelvin temperature
B is the bandwidth of the AC voltage measurement
R is the resistance of the resistor
The factor of 4 comes from the dimensional degrees of freedom accorded to the charges in the resistor and that only the axial component of movement contributes to output noise. The derivation is left up to the student.
For example, a 1 kΩ resistor will generate:![]()
in a 100 MHz bandwidth at 22ºC
The thermal noise in a 50Ω environment at room temperature is -174 dBm in a 1 Hz bandwidth. An RF engineer should memorize this number. This comes from the noise power calculation:![]()
See this and more important radio frequency charts and formulas in this comprehensive application note.
Related Post
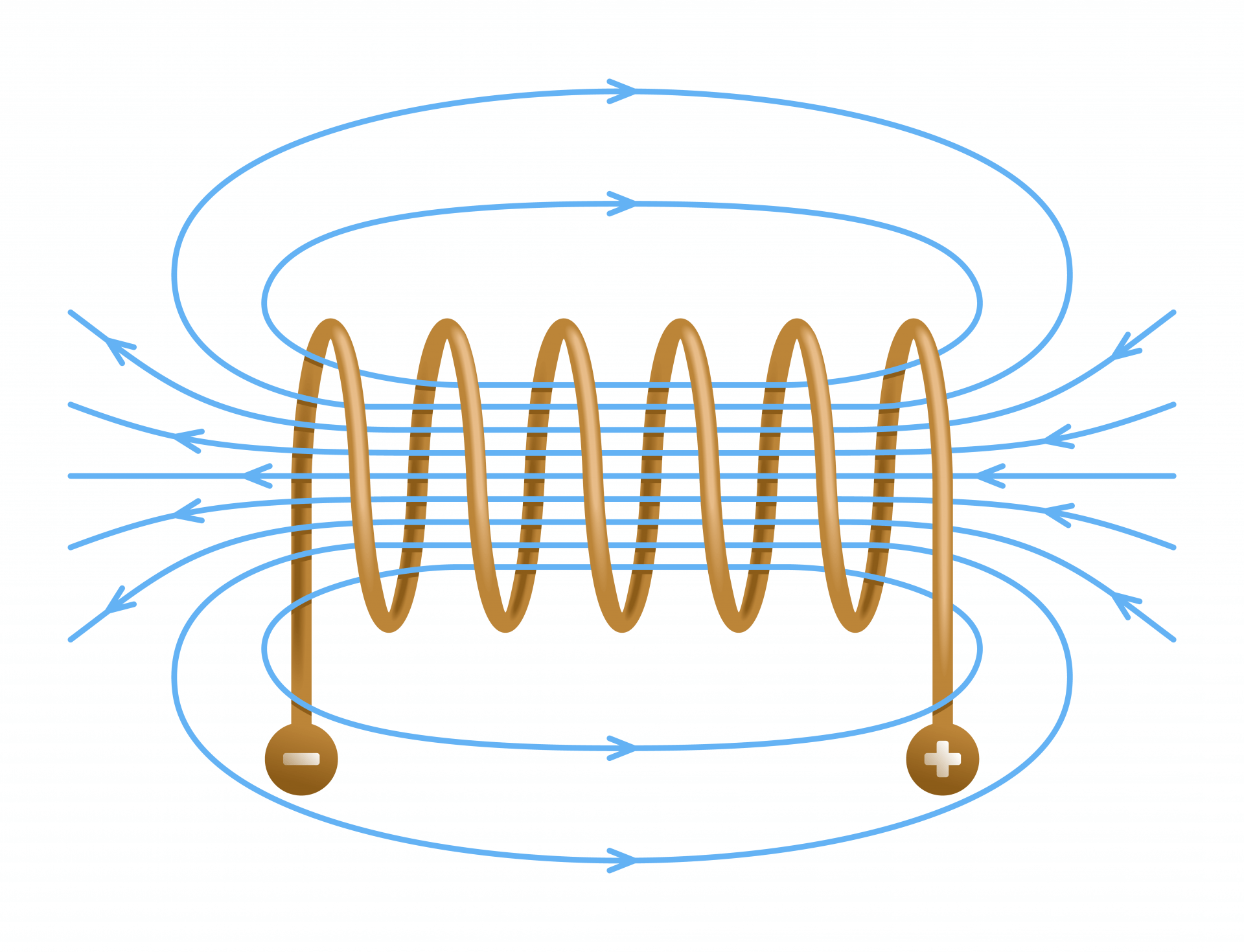
What is the Inductance of a Solenoid (Coiled Wire)?
July 24, 2023
The inductance of a solenoid is approximately: Where r is the radius in inches, l is the length in inches, and n is the number of turns. It may also be calculated more precisely from this equation (from Ampere’s Law) with similar results: Where μ is free space permeability 4π*10-7 H/m n is the number of turns A is the cross-sectional area in m2 l is the length of the coil in meters See this and more important radio frequency charts and formulas in this comprehensive application note.
Useful Radio Frequency Engineering Formulas and Charts
February 9, 2023
This application note is a collection of essential formulas and charts for Radio Frequency Engineering.
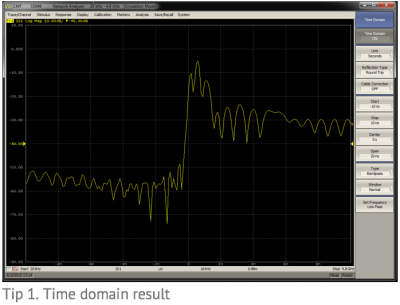
Getting Started with the CMT VNA: Top 10 Tips and Tricks
February 14, 2018
The examples created in this document are based on the S5048, but apply to most of the Copper Mountain Technologies VNAs in a similar way. These tips will help you use your VNA with ease and help you get more intuitive results.


