By Brian Walker, Sr RF Engineer, SME

The trace math feature of a Copper Mountain Technologies Vector Network Analyzer (VNA) is very useful. This application note will give a few examples of its use.

Getting Started with Trace Math in VNA Software

On the VNA UI, click on the S-Parameter callout in the top left corner.

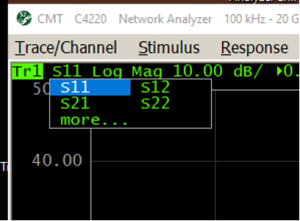
Choose “more…”

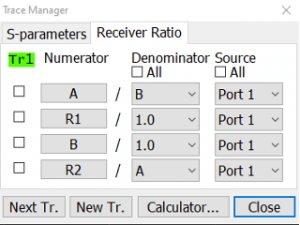
This panel can be used to operate on the trace highlighted in green. If another active trace should be used, click on “Next Tr.” to switch to it. “New Tr.” may be used to add a new trace and switch to it.

Column one lists the four VNA receivers. R1 and R2 are the reference receivers, which monitor the signals leaving ports 1 and 2, respectively. A and B receivers monitor signals entering ports 1 and 2, respectively. Selecting “1” for the denominator and clicking the checkbox will show the signal on that receiver.

Selecting A/R1 with the Port 1 source active allows you to view an uncorrected version of S11. Similarly, selecting B/R1 with the Port 1 source active will enable you to view an uncorrected version of S21. Uncorrected S12 is A/R2, and S22 is B/R2, both with Port 2 active.

Examining the phase and magnitude relationship between two signals entering ports 1 and 2 is also possible. First, turn off the internal signal source by navigating to Stimulus/Power and clicking on RF Out. Click on “Start” in the lower-left corner of the UI, switch to “Center,” and enter the frequency that will be applied. In the lower-right corner, set the span to 0. Consider setting the IF bandwidth as wide as possible to ensure that the external signal is captured. Choose A/B or B/A on the calculator to see the ratio between the two signals. It doesn’t matter which source port is selected since the power is turned off. The two input signals must be the same frequency, perhaps receiving a signal with two antennas or looking at the phase shift on the two output ports of a 90-degree hybrid.

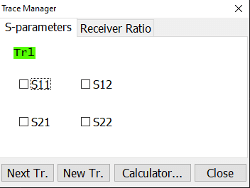
Choosing the “S-parameters” tab allows users to change to the standard S-parameters S11, S12, S21, or S22.

Basic Functions

Pushing the “Calculator…” button gives access to the trace calculator’s next “Basic” level. In this calculator, traces and S-parameters may be manipulated in useful ways.

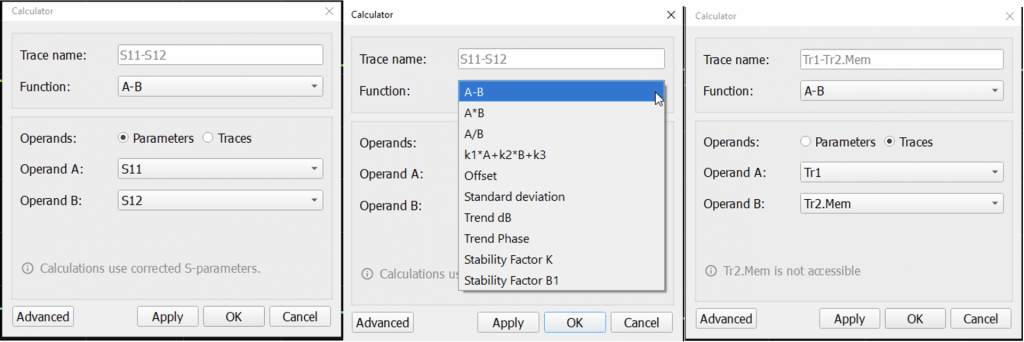
The first few selections perform operations on two linear terms. These terms can be S-parameters, traces, or trace memories. Function A-B subtracts the magnitude of two terms. A*B performs a complex multiplication, A/B complex division. The next function performs a weighted sum of two terms and adds an offset.

The Offset function adds or subtracts a dB value from a term and/or adds a phase offset in degrees. The Standard Deviation function performs a standard deviation function on the linear value of the chosen term. The Trend dB function adds a linear dB slope and an offset to the term. The Trend Phase function performs similarly for the phase of the term in degrees.

The last two functions are stability factors, which are useful for evaluating an amplifier’s stability. This information is very important for an RF designer. Some off-the-shelf amplifiers are not unconditionally stable and may need additional components to prevent spontaneous oscillation. For example, the MiniCircuits PGA-103+ is an exceptional amplifier with 11 dB of gain, 0.6 to 0.9 dB Noise figure, and a respectable +45 dBm OIP3. The S-parameters can be downloaded from the website and loaded into the VNA. Using the VNA UI, Save/Recall/Load Data from Touchstone File/To S-Parameters, and choose the S-Parameters for the amplifier. Set the trace type to S21 Lin Mag 0.100 U/ 0.800 U.

Open the calculator, select Stability Factor K, and apply. The Rollet stability factor will be displayed. An amplifier is expected to be stable for K values greater than one.

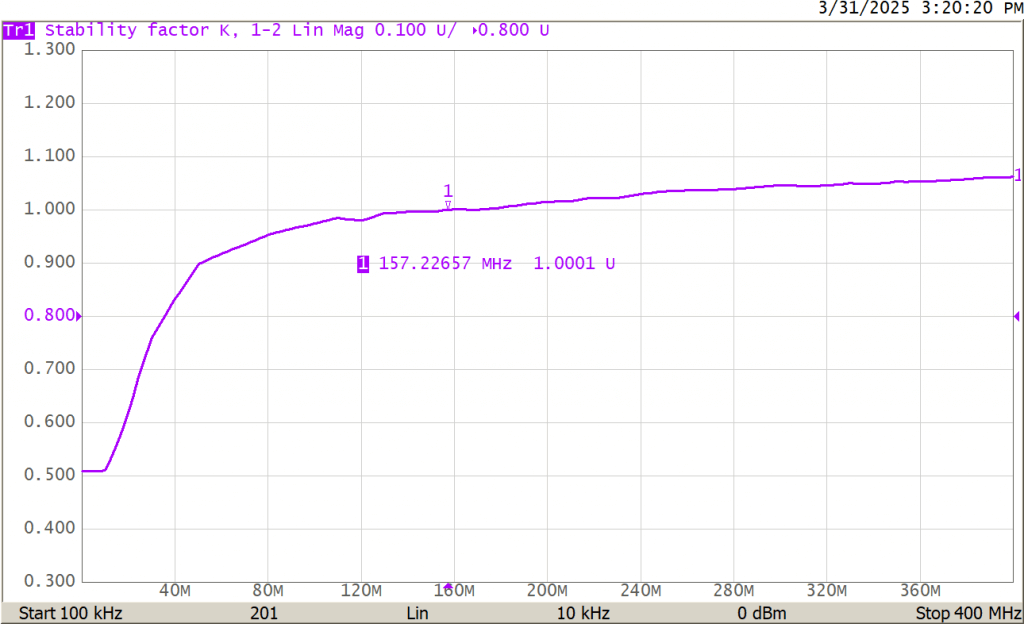
Figure 1 – K Stability Factor

Here, the K stability factor is less than one below 157 MHz in Figure 1, indicating potential instability in that region. The data sheet for the PGA-103+ recommends adding a 620 nH inductor, a 150 ohm resistor and a 330 pF capacitor all in series to ground and attached to the input of the amplifier as shown below.

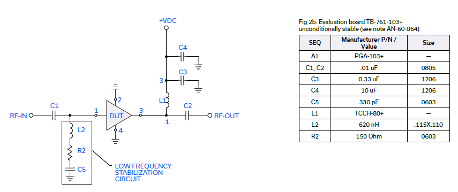
Adding the suggested network results in a K factor greater than 1, as shown in Figure 2 (violet trace), and the amplifier should now be unconditionally stable.

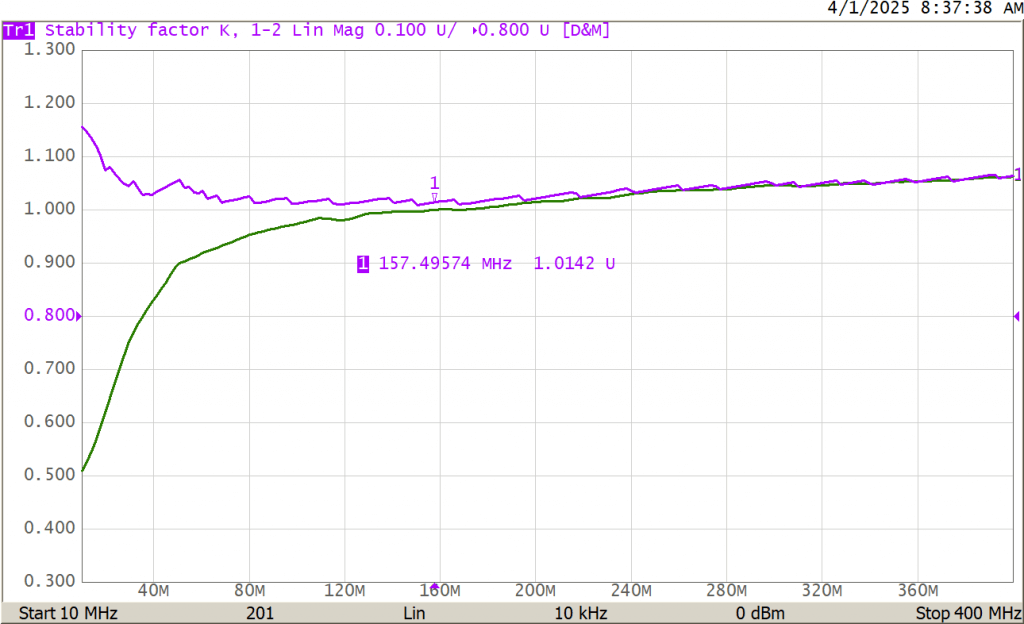
Figure 2 – Stabilized amplifier

As a follow-up, the VNA can measure the amplifier’s performance in its final circuit configuration, and stability may be checked once again in situ. If the measurement is made with soldered-in pigtails, it would be beneficial to de-embed them using the Automatic Fixture Removal program (AFR) from Copper Mountain Technologies.

Finally, for guaranteed stability, it is necessary but not sufficient that the stability factor K be greater than one; An additional stability measure B1 should also be greater than zero. This is the last choice on the calculator menu.

The Advanced Calculator

Pressing the “Advanced” button takes us to the advanced calculator UI.

The “Functions” menu contains a selection of trigonometric, log, and other functions. The “Traces” menu allows for the selection of different kinds of trace data. To make sense of the trace designations, refer to the block diagram of Figure 3.

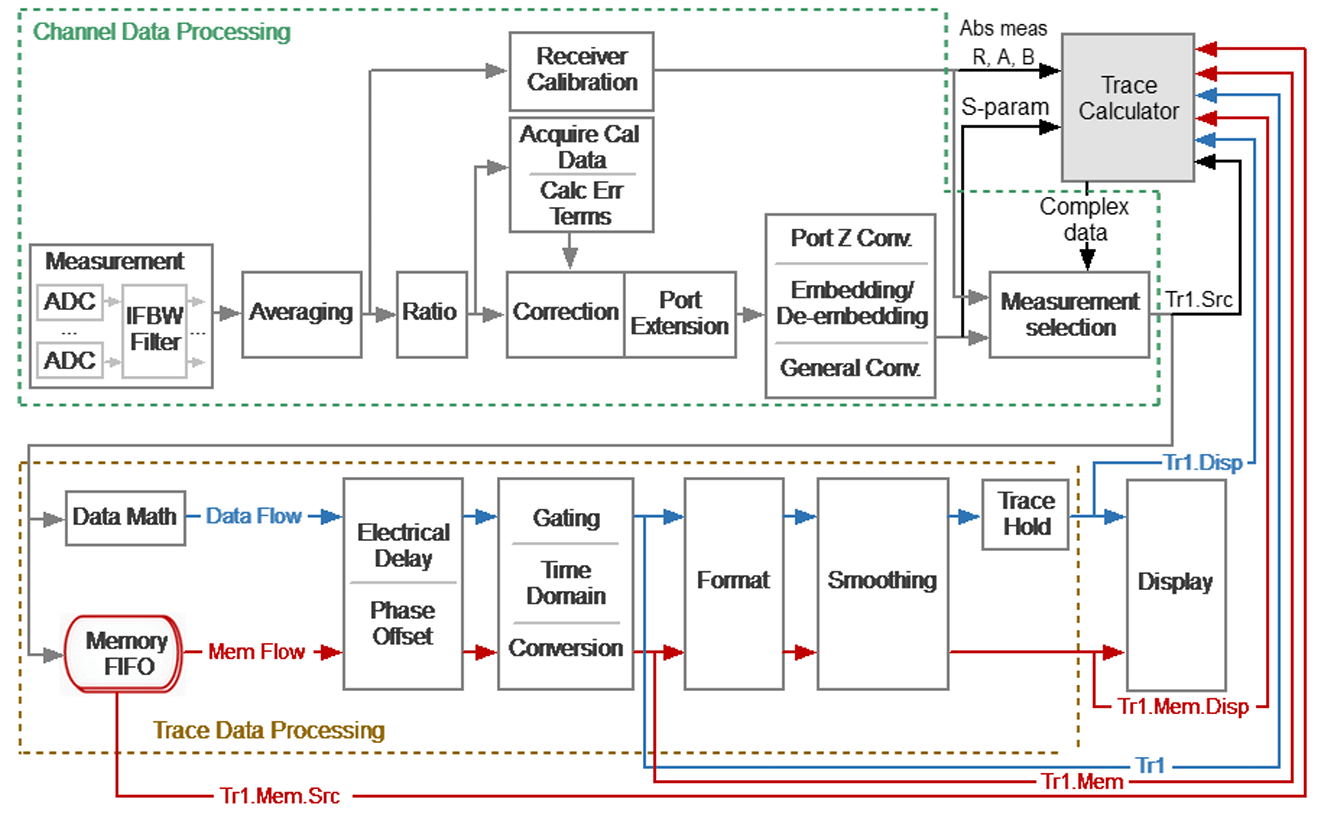
Figure 3 – Data types

For example:

Tr1.Src:
Calibrated complex reflection coefficients, potentially with Port Extension, Port Z conversion, Embedding or De-Embedding, or General Conversion

Tr1:
Tr1.Src with added potential Data Math, Electrical Delay or Phase Offset, Time Domain, Time Domain Gating, and Impedance Conversion, but no Formatting or Smoothing.

Tr1.Mem:
Outputs the memorized Trace 1 data with the same parameters as Tr1

Tr1.Disp:
Tr1 with added Formatting and potential Smoothing applied.

The next column allows for the choice of S-parameters or raw receiver data. The designation R1_1 refers to the Port 1 reference receiver, which monitors the incident output signal with the stimulus switched to exit Port 1. T1_1 refers to the Port 1 reflection receiver, which monitors signals entering Port 1, with the stimulus switched to exit Port 1. R1_2 seems silly since there should be no signal on the Port 1 reference receiver when the stimulus is switched to Port 2, but it is helpful for some special cases involving a Direct Receiver Access VNA.

Differential Calculation

A 2-Port VNA may be used to measure differential return loss by calculating the differential parameters from unbalanced measurements made by each port. That is:

Enter this into the calculator as (S11+S22-S21-S12)/2. The S-parameters may be chosen from the menu selection, typed into the Expression field by hand, or pasted from a text document. This would allow the user to examine a twisted pair and see the differential return loss. Additionally, the time domain analysis function, a standard feature in most CMT VNAs, may be used to evaluate reflection vs. distance along the twisted pair to detect any breaks or abnormalities.

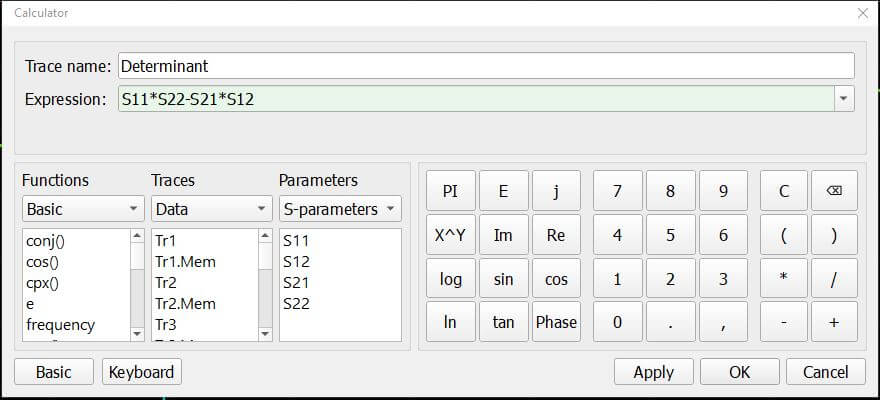
The S-Parameter Determinant

The magnitude of the determinant of the S-parameter matrix S11*S22-S21*S12, tells us something about a 2-port network. If it is equal to one, then the network is lossless. A magnitude greater than one for an amplifier with potential instability. A magnitude less than one typically indicates power loss.

Helpful Hint: It is recommended to keep a text document with a set of favorite functions which can be cut and pasted into the calculator expression field.

Pi-Network Extraction

Consider the Pi network in Figure 4. The three admittances, Y1, Y2, and Y3, can be extracted from the network’s Y-parameters.

The Y-parameters can be found from the S-parameters easily (with Y₀ = 1/50).

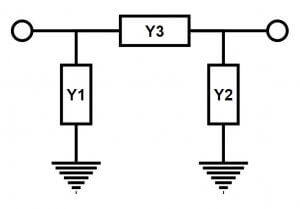
Figure 4 – PI Network

For a Pi-network:

Y₁ = Y₁₁ + Y₂₁

Y₃ = -Y₂₁

Y₂ = Y₂₂ + Y₂₁

In the calculator (for 50 ohm S-parameters):

Y1 = (1/50)*((1-S11)*(1+S22)+S12*S21-2*S21))/(S11*S22-S12*S21)

Y3 = (1/50)*(2*S21)/(S11*S22-S12*S21)

Y2 = (1/50)*((1+S11)*(1-S22)+S12*S21-2*S21))/(S11*S22-S12*S21)

If Y1 were known to be a capacitor, one could plot the value of that capacitor:

C1 = Y1/(2*pi*frequency)

C1 = (1/(2*PI*frequency))*(1/50)*((1-S11)*(1+S22)+S12*S21-2*S21))/(S11*S22-S12*S21)

If Y3 were known to be an inductor, one could extract that value as well:

L3 = -1/(2*PI*frequency*Y3)

L3 = (-1/(2*PI*frequency))*1/((1/50)*(2*S21)/(S11*S22-S12*S21))

It is easy to see how this method could be used to extract lumped element values from measured S-parameters. The location of the reference plane is crucial, however; it must be located right at the component position. Port extension or de-embedding should be employed to ensure this.

Instead of calculating the Y-parameters, one could use General Conversion under the Analysis menu to display Y11, Y21, and Y22 on three traces. Then, the VNA can do that conversion, and the previous calculations can be performed by choosing traces Tr1, Tr2, or Tr3 as needed.

T-Network Extraction

To extract a T-network as in Figure 5, use Z-parameters.

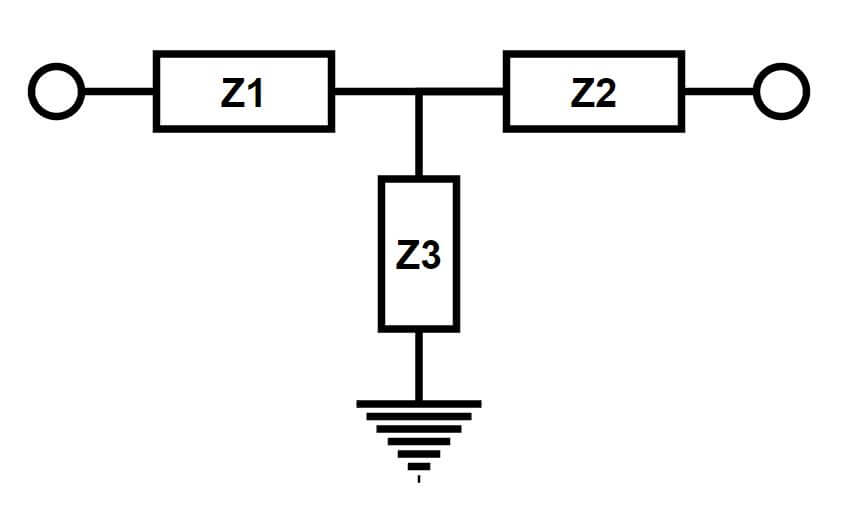
Figure 5 – T-Network

Where:

The Z-parameters may be calculated from S-parameters as follows (with Z₀=50):

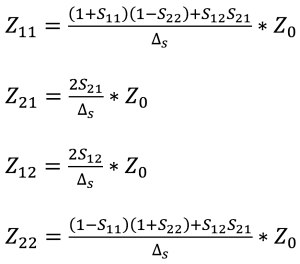
Where

Then:

Z1 may be entered in the calculator as follows:

50*((1+S11)*(1-S22)+S12*S21-2*S21)/(S11*S22-S12*S21)

And Z2:

50*((1-S11)*(1+S22)+S12*S21-2*S21)/(S11*S22-S12*S21)

And Z3:

50*2*S21/(S11*S22-S12*S21)

These two methods might be used to better understand a device. If the S-parameters of an amplifier are known, the first element of the T-network, Z1, might be the component’s internal bond-wire inductance. An RLC model of an inductor, containing all parasitic values could be created from its S-parameters and used for more accurate simulation. The primary, secondary and mutual inductance of a transformer can be found by modeling it as a Pi-network and finding Y1, Y2 and Y3.

Conclusion

These are just some calculations that might be performed using trace math. We’ve seen how the amplitude and phase of two signals may be compared, how the stability of an amplifier can be verified, how differential measurement conversion is done, and how Pi or T network models might be generated from S-parameters. Many more applications are possible, limited only by the user’s creativity. Trace math is just one of many advanced features available on a Copper Mountain Technologies VNA. Visit our website to see our lineup of equipment and check out our other application notes, videos, and webinars to help you better understand Vector Network Analysis and get more out of your measurements.